network
"Die offene Vernetzung von Kompetenzen ist die Alternative zur inkompetent gewordenen einsamen Vermassung." Vilem Flusser [1]
|
|
For the classic arts it sounds like an affront: cutting up a picture, shipping separately the
pieces in packets maybe on different routes and finally putting them smoothly together somewhere else. That is no scenario of iconoclasm, but just what the
WWW has made
possible (internet packet routing).
The basic idea of the development of the WWW was to share information. Only fifteen years before the WWW was still a project at the CERN/Geneva. Today it is the standard for the worldwide network communication.
|
|
The Imachinations also reflect the short history of the internet. The popular break through for the WWW happened by integrating pictures to the browsers. What happens, when images can be shared as information? (more...)
Scientists have used the internet, e.g. email services, long before the invention of the WWW. But this internet services were bound to specific hard- and software platforms. So the basic idea of the WWW was to create a cross platform internet. Today the WWW constiutes not only for scientists a new quality of cooperation and exchange of information (e.g. arxiv.org).
Hyperlinks as revolution
But this world wide network also caused a mental revolution in computer science: Information results not only from the content itself, but mainly from the links speaking how the content is related to other content. Search engines like google are so succesfull, because they just focus the links (more...)
|
|
Molecular Networks
The idea of networks becomes relevant in molecular biology, too. A crucial question is how proteins or genes are related. Bioinformatics software like Cytoscape can visualize molecular interaction networks and integrate these interactions with gene expression profiles and other state data.
|
 |
Grids - networks become a giant computing machine
Networks also enable to join single computers to a so called grid. This idea of a grid is analogous to electric power network (grid) where power generators are distributed, but the users are able to access electric power without bothering about the source of energy and its location. Computational grids enable the sharing, selection, and aggregation of a wide variety of geographically distributed computational resources and presents them as a single, unified resource for data intensive computing applications (e.g, molecular modelling for drug design or high energy physics).
A grid differs from a cluster by its decentralized organization: A node in a grid has its own resource manager and don't aim for providing a single system view.
|

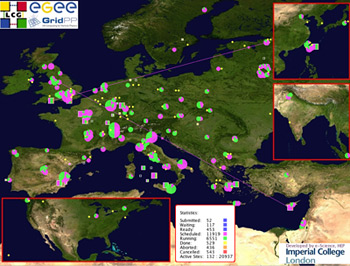
Upcoming high energy physics experiments like the LHC starting currently at CERN couldn't be managed without a grid.
|
Wireless
Dave Hughes alternative wireless projects link remote places in Alaska or at the Himalya to the web. At the right: the highest cybercafe of the world at 5300 m close to the Mount Everest
|

"cybercafe' at Mt. Everest
|
Percolation
Perculation theory has found broad application to porous media. But it also helps to calculate the stability of networks. (more...)
|

scale-free network by Barabási
|
Theory links
Albert-László Barabási's & Zoltán Toroczkai's network image gallery
http://computer.org/internet/v2n1/cailliau.htm
Interview with the former CERN IT-chief Robert Cailliau, who developed with Tim Berners-Lee the basic ideas for the WWW. In this interview he talks also about the first graphics in the WWW, scalable postscript (ps) data.
http://www.youtube.com/watch?v=x2GylLq59rI
Read more about the short history of the internet by Richard T. Griffiths.
|

high speed communication for scientific purposes even in antarctica (by AWI)
|
Networks meet art & design
Diagrams can show art history and theory as a network of interrelated concepts, definitions and models like the network diagram of ars electronica by Gerhard Dirmoser:
"25 jahre ars electronica - ein überblick als gedächtnistheater"
|
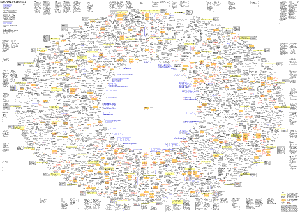
network diagram of 25 years of ars electronica by Gerhard Dirmoser
|
Visualcomplexity, a project of the Portuguese designer Manuel Lima, currently joins more than 250 (!) network diagrams:
|
 |

"history flow", visualization by Martin Wattenberg (IBM) of the network dynamics creating a wiki-page
|
|
[1] Flusser, Vilém: Vom Subjekt zum Projekt. Menschwerdung, Bernsheim-Düsseldorf 1994, p.73
|
|




























